Ayudantías Departamento de Matemáticas Usach
lunes, 16 de julio de 2012
domingo, 8 de julio de 2012
Gauss y la integral Gaussiana
La Integral de Gauss
Función gaussiana 
. El área encerrada bajo esa curva con el eje x es 
. El área encerrada bajo esa curva con el eje x es
En matemáticas la integral de Gauss, integral gaussiana o integral de probabilidad, es la integral impropia de la función gaussiana 
sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es:
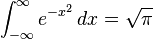
Esta integral tiene amplias aplicaciones, incluyendo normalización, en teoría de la probabilidad y transformada continua de Fourier. También aparece en la definición de la función error. A pesar de que no existe ninguna función elemental para la función error, como se puede demostrar mediante el algoritmo de Risch, la integral Gaussiana puede ser resuelta analíticamente con las herramientas del cálculo. O sea, no existe una integral indefinida elemental para
pero si es posible evaluar la integral definida 
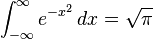
sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es: Esta integral tiene amplias aplicaciones, incluyendo normalización, en teoría de la probabilidad y transformada continua de Fourier. También aparece en la definición de la función error. A pesar de que no existe ninguna función elemental para la función error, como se puede demostrar mediante el algoritmo de Risch, la integral Gaussiana puede ser resuelta analíticamente con las herramientas del cálculo. O sea, no existe una integral indefinida elemental para
pero si es posible evaluar la integral definida
Cálculo de la integral
La forma más común de calcular la integral de Gauss en el plano R2 es mediante la integración doble en el sistema cartesiano de coordenadas, para después hacer un cambio de coordenadas a coordenadas polares y calcular el valor. Se procede de la siguiente manera:
sábado, 7 de julio de 2012
Suscribirse a:
Entradas (Atom)