jueves, 22 de marzo de 2018
domingo, 31 de agosto de 2014
La garra del León
Ex ungue leonis
En 1696, Johann Bernoulli planteó ante los matemáticos de la Royal Society dos abtrusos problemas matemáticos. Más que de un pedido de colaboración entre científicos, se trató de una especie de concurso: Johann ofreció como premio, a quien fuese capaz de dar las soluciones de ambos, un libro científico de su biblioteca personal. Bernoulli sabía que muchos de los miembros de la Sociedad ambicionaban el ejemplar, que a la sazón era carísimo: costaba nada más ni nada menos que cuatro chelines, toda una fortuna para la época. Aunque la mayor parte de los miembros de la Royal Society eran genios absolutos, su excelencia científica no los había hecho ricos, y ninguno de ellos disponía de peculio suficiente para comprarlo, ni siquiera los que ostentaban títulos de Sir o Lord.
Bernoulli sabía que, con el aliciente del libro, todos pondrían manos a la obra con ahínco y tenacidad. Estableció un plazo máximo de seis meses para presentar las soluciones, y se puso a esperar.
Entre los participantes del certamen se encontraban: Robert Hooke, matemático y descubridor de la célula; Sir Edmond Halley, físico, matemático y astrónomo, descubridor de la periodicidad de los cometas, que encontró estudiando al que hoy lleva su nombre; Gottfried Leibniz, coinventor, junto con Newton, del cálculo infinitesimal (lo desarrollaron independientemente y sin colaborar entre sí: la diferencia estuvo en que Leibniz lo publicó de inmediato y Newton no lo hizo hasta mucho después), Sir Christopher Wren, Christiaan Huygens y otras figuras de similar talento. Por causas no muy bien establecidas, Newton no estaba presente en el lanzamiento del desafío y no se enteró del concurso en ese momento.
Bernoulli esperó y esperó... Esperó y esperó.
Esperó.
Los seis meses transcurrieron, y sólo Leibniz había encontrado la solución a uno de los dos problemas. Como las bases decían que el ganador debía resolver ambos, Bernoulli extendió el plazo por seis meses más, en la esperanza de que alguien consiguiera la solución al segundo.
El año transcurrió, y nadie pudo mejorar la solución de Leibniz al primer problema y mucho menos resolver el segundo.
Molesto por su fracaso, Leibniz sugirió a Bernoulli que se solicitara el auxilio de Newton. Johann comisionó entonces a Halley —muy amigo de Newton— para que le entregara los dos problemas.
El 29 de enero de 1697 Halley visitó a Newton. Recuerda con asombro la entrevista con Newton, su distracción extrema y su falta de concentración en estos términos: "Llegué a su casa a las dos de la tarde. Él estaba encerrado en su estudio, y la servidumbre tenía estrictas órdenes de no molestarlo ni abrir la puerta por ningún motivo. Por lo tanto, me senté afuera a esperar que saliera. Rato después, el ama de llaves trajo el almuerzo de Newton en una bandeja, y lo dejó en el piso, frente a la puerta. Las horas pasaron. A las seis de la tarde, yo sentía un hambre atroz, y me atreví a devorar el pollo de la bandeja. Cuando Newton por fin abrió la puerta, miró los huesos del pollo en la bandeja, me miró a mí y exclamó: —¡Qué distraído soy! ¡Pensé que no había comido!".
Halley explicó a Newton la situación y le entregó la carta de Bernoulli conteniendo los dos problemas. Newton dejó la carta sobre un escritorio y despidió rápidamente a Halley, explicando que "luego echaría una ojeada a los problemas".
Los dos problemas que habían tenido ocupados a todos los miembros de la Royal Society durante más de un año, en los cuales habían fracasado matemáticos del calibre de L´Hôpital, David Gregory y Varignon, los dos problemas de los cuales Leibniz sólo había encontrado una tortuosa solución para uno de ellos, fueron resueltos por Newton en diez horas.
A las cuatro de la mañana del día siguiente los tenía listos, y a las ocho envió sus soluciones en una carta sin firma al presidente de la Royal Society. Sus desarrollos eran tan perfectos y elegantes, que las soluciones de Newton fueron publicadas —también en forma anónima— en el número de febrero de 1697 de Philosophical Transactions. Newton había resuelto en una noche dos problemas que a cualquier otro matemático le hubiesen llevado la vida entera.
Bernoulli, impresionado por la elegancia de las soluciones de Newton, no tuvo dificultad en identificar al autor: "Es Newton", afirmó. "¿Cómo lo sabe?", le preguntaron. "Porque reconozco las garras del león (Ex ungue leonis)".
Hay quien dice que tanto Johann como su hermano Jacob Bernoulli consiguieron resolver el primero de los dos problemas, de modo que sólo Newton, Leibniz y los dos Bernoulli encontraron una solución. No me sorprende, porque está demostrado que ellos eran las cuatro únicas personas que podían manejar, en la década de 1690, las complejidades y sutilezas del cálculo integral y diferencial, imprescindibles para la solución del primer problema.
La solución de Leibniz era muy trabajosa. La de Johann Bernoulli era bastante elegante pero muy particular. La de su hermano mayor Jacob era ripiosa y avanzaba con dificultad, muy elaborada y aburridísima, pero más general que la de Johann.
Creo que, a esta altura, huelga decir que la de Newton es la mejor, incluso hoy en día. Breve, simple, elegante, entretenida y general, nadie ha podido superarla.
El segundo problema, por su parte, derrotó a todos, salvo, por supuesto, a las garras del león.
Los dos problemas de Bernoulli
Los dos problemas que Bernoulli propuso a la Royal Society lo habían preocupado durante años.
Ambos tienen la particularidad de que se enuncian fácilmente, pero esta aparente simpleza oculta complejidades tan tremendas, que sólo la sobrehumana clarividencia de Newton pudo desentrañar en pocas horas.
Primer problema: "Determine la braquistócrona".
Segundo problema: "Encuentre una curva tal que si se traza una línea desde un punto dado O, que corte a la curva en P y en Q, entonces OP´ + OQ´ sea una constante".
Newton no sólo encontró la mejor solución para el primero, sino que resolvió el segundo y encontró para éste una solución general.
La Helena de los geómetras
Hagamos rodar un círculo sobre una superficie plana y observemos la trayectoria que describe un punto cualquiera del mismo.
En otras palabras, si marcamos el punto más bajo de un círculo que descansa sobre una línea horizontal, y movemos el círculo, haciéndolo rodar (sin fricción ni rozamiento), el punto marcado en el círculo se desplazará hacia arriba, alcanzará una altura máxima —igual al diámetro del círculo—, y comenzará a descender hasta tocar de nuevo la línea horizontal, en un lugar situado a una distancia del punto original igual a la circunferencia del círculo.
Pues bien: la curva descripta por el punto en cuestión, que se repite tanto como sigamos haciendo girar el círculo, se llama cicloide.

La maravillosa cicloide
La cicloide tiene varias particularidades, como la de describir una caída libre gravitatoria. Además, es una de las pocas curvas que funcionan de la misma manera tanto en la mecánica newtoniana como en la relatividad general, en términos de su tiempo propio de caída libre.
La cicloide es una curva tan particular, que fue estudiada por todos los matemáticos importantes, en todas las épocas. Provocó tantas querellas, guerras, peleas y reyertas entre ellos, que se la conoce como la "Helena" de los geómetras.
El primero en interesarse por ella fue Charles Bouvelles, quien la creyó un medio mecánico para lograr la cuadratura del círculo.
Más tarde, Galileo Galilei y su alumno Viviani estudiaron la cicloide, obteniendo a partir de ella un método de construcción de tangentes. Galileo se dio cuenta, además, de que la cicloide era el mejor de los perfiles posibles para construir los arcos de los puentes.
El sabio italiano escribió en 1640: "He estado queriendo describir esa línea curva durante más de cincuenta años, y la admiré por su curvatura, ideal para soportar los arcos de un puente. Hice varios intentos para demostrar que el espacio incluido entre ella y su cuerda era tres veces más grande que el círculo que describía la cicloide, pero estaba errado. No era tres veces mayor, aunque la cifra no estaba lejos de tres".
Mas Galileo se equivocaba: de hecho, la superficie del área definido por la cicloide es tres veces la del círculo generatriz. Tal extremo fue demostrado al mismo tiempo por Torricelli, Roberval y Blas Pascal. El error de Galileo se debió a que, en vez de calcular la superficie por métodos geométricos, trató de medir el área construyendo modelos de cicloides y pesando los mismos.
Mersenne hablaba con todos sus corresponsales de las extrañas propiedades de la cicloide, y, precisamente, su alumno Roberval fue uno de los que demostró la superficie del arco cicloidal.
Poco tiempo después se encontró el centro de gravedad y se descubrieron también los volúmenes de los sólidos que se obtienen rotando una cicloide alrededor de su base y de su eje.
En toda esta investigación se ocuparon los más importantes matemáticos de la época, incluyendo al gran René Descartes.
Ganando la Cátedra de Matemáticas del College Royal en 1634 gracias a sus técnicas investigativas aplicadas a la cicloide, Roberval consiguió mantener el cargo durante cuarenta años. Mas la "Helena de los geómetras" metería la cola...
El francés había llegado a su puesto mediante concurso público, que incluía una competición matemática trienal, pero el reglamento no exigía explicar los métodos utilizados. El titular de una cátedra (que era quien elegía los problemas del concurso) tenía, pues, muy buenas razones para mantener sus procedimientos ocultos, porque muy bien podían ser utilizados por otros para desbancarlo tres años más tarde.
Roberval, al no querer explicar cómo había llegado a sus conclusiones, perdió el derecho de precedencia sobre varios descubrimientos, entre ellos la superficie del arco de la cicloide, y se vio envuelto en numerosas querellas.
Uno de los que lo demandó por el asunto de nuestra Helena fue Evangelista Torricelli, quien había publicado en 1644 una explicación completa (obtenida independientemente) del área y las tangentes de la cicloide. No es sorprendente que Torricelli hubiese llegado por sí mismo a las mismas conclusiones, ya que había sido asistente de Galileo, quien posiblemente le transmitió sus conocimientos sobre el tema.
El concurso de Pascal
Un día de 1658, Blas Pascal se despertó con un horrible dolor de muelas, y comenzó a pensar en la cicloide para ver si desconcentrarse del dolor lo ayudaba en algo. Mágicamente, el dolor se fue, y, en agradecimiento, el matemático dedicó los siguientes ocho días a estudiar la cicloide en profundidad. Luego de redescubrir casi todo lo que los anteriores habían hallado con respecto a esta curva y de encontrarle unas cuantas propiedades nuevas, Pascal decidió promover un concurso que consistía en resolver algunos problemas de cicloides. Los dos mejores trabajos serían premiados, y actuarían como jurados Roberval y el mismo Pascal. Recibieron dos respuestas correctas, firmadas una por Wallis y la otra por Lalouvere, mas los jueces consideraron que no cumplían las expectativas y los premios fueron declarados desiertos.
¿Qué hizo Pascal? Publicó sus propias soluciones sobre la cicloide, además de un ensayo titulado "Historia de la Cicloide" donde tomaba partido por Roberval en su vieja disputa con Torricelli acerca de la precedencia de los descubrimientos sobre la sorprendente curva.
Sin embargo, toda esta embarazosa cuestión terminó rindiendo sus frutos: Christiaan Huygens, que estaba tratando de mejorar su diseño de relojes (su gran pasión, aparte de la matemática), se percató de que el período de oscilación del péndulo no es del todo independiente de la amplitud de su recorrido. Inspirado en el asunto de Pascal y el concurso, el holandés pensó en qué pasaría si el péndulo era obligado a seguir una trayectoria cicloidal. Previsiblemente, descubrió que ese sistema sí era perfectamente independiente de la amplitud. Huygens había descubierto que las cicloides son "tautócronas", es decir que el tiempo que una partícula tarda en recorrer la distancia desde cualquier punto de la cicloide hasta el punto más bajo de la curva es siempre el mismo, no importa si lo iniciamos en la parte más alta de la curva, en la mitad o desde un punto muy cercano a la base.
La braquistócrona
No terminó así el asunto, puesto que llegamos ahora a la noche de 1696 en que Johann Bernoulli propone a los honorables miembros de la Royal Society que determinen la braquistócrona, con el invaluable libro de cuatro chelines como acicate.
"Dados dos puntos A y B sobre un plano vertical, débese determinar la trayectoria AMB de una partícula M a lo largo de la cual, descendiendo por su propio peso, M se moverá de A a B en el menor tiempo posible". En pocas palabras, como dijimos, "determine la braquistócrona".
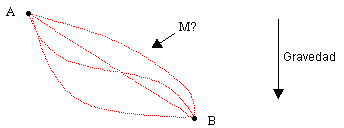
Determine la braquistócrona
Si creemos a Johann (y no a su hermano), éste descubrió algo que lo movió a escribir, en enero de 1697, una carta a Huygens en la que decía: "Te vas a quedar petrificado cuando te diga que la cicloide es, precisamente, la braquistócrona solicitada". Es decir, que el camino que utiliza un tiempo más corto para un móvil que cae por gravedad tiene forma de cicloide.

Camino más rápido entre A y B: una cicloide
Como se ve en el diagrama anterior, el sentido común (que normalmente conduce a error), nos dice que el camino más rápido para que la bolita pase de A a B es un plano inclinado AB. Sin embargo, el braquistócrono es la cicloide ilustrada. Claro, Newton, sabía que la mayor aceleración en la parte más vertical de la curva aceleraría el móvil más que la aceleración constante de un plano inclinado, lo cual demostró utilizando el cálculo infinitesimal. De hecho, su solución de este problema se considera el primer resultado exitoso de sus "fluxiones" (él llamaba así al cálculo).
Así como los hermanos Bernoulli se pegaban entre ellos para ver quién descubría las cosas antes, y como Leibniz decía que él había descubierto primero el cálculo infinitesimal (aunque Newton, como dije, lo había hecho antes en silencio), sucedió que Johann y su hermano apoyaban a Leibniz en su reclamo. Hay quien dice, entonces, que el envío del desafío al viejo león fue una forma de burlarse de él, pensando que no sería capaz de resolverlo. La ladina carta de Bernoulli, inocentemente entregada por Halley, decía: "Hay pocos que son capaces de resolver mis excelentes problemas, especialmente muy pocos entre esos matemáticos que han visto crecer su fama a través de dorados teoremas que ellos creen que nadie más conoce, aunque hayan sido previamente publicados por otros...". Era, en realidad, una directa acusación (injusta, además) a Newton de plagiar el trabajo de Leibniz.
Halley afirma que Newton, ofendido, no durmió hasta tener resuelto el asunto a las cuatro de la mañana, sabedor de que era imposible que un problema resuelto por Bernoulli y Leibniz le permaneciera inaccesible.
Newton diría más tarde, consciente de que su solución era mejor que la de los otros: "Me molesta que me desafíen e insulten algunos que no son más que extranjeros en la matemática...".
Bernoulli contaba con una ventaja sobre Newton: el inglés resolvió la braquistócrona sólo con un lápiz, un papel y su cerebro, mientras que Bernoulli lo había hecho a través de la observación experimental, estudiando la trayectoria de un rayo de luz a través de un medio no uniforme. Demostró cómo esta trayectoria se relacionaba con el problema mecánico de un objeto moviéndose a velocidades variables y comparó la versión óptica con la mecánica.
La comparación era que en un caso, la densidad óptica es inversamente proporcional a la velocidad, en tanto que la densidad de un medio físico guarda la misma proporción con la velocidad de caída libre de un objeto. "De esta forma", escribió el ególatra Bernoulli, "he resuelto dos difíciles problemas: uno óptico y otro mecánico...". Por supuesto que su solución se basa en la ley de Galileo de cuerpos en caída libre (según la cual las velocidades de caída son la raíz cuadrada de la altura). También da crédito a Huygens: "Antes de terminar, expresaré mi admiración por el hecho de que la tautócrona de Huygens y mi braquistócrona sean, inesperadamente, la misma curva. Encuentro especialmente admirable que esta coincidencia sólo es posible bajo la hipótesis de Galileo, de lo que obtenemos una prueba de que aquélla es correcta. La naturaleza tiende siempre a actuar de la manera más simple posible, y así permite, en este caso, la existencia de una sola curva que cumple ambas funciones, condiciones bajo las cuales, con cualquier otra hipótesis, necesitaríamos dos curvas...".
Bernoulli era un genio, pero no uno incomparable. No tenía idea, por ejemplo, de que, además de las propiedades que tanto lo entusiasmaban, la cicloide, aparte de ser la tautócrona y la braquistócrona, es la única curva posible que describe la caída libre gravitacional radial contra el tiempo propio en la Teoría de la Relatividad General. En la frase citada más arriba, además, puede reconocerse el puntapié inicial del Principio de Maupertuis (o "Principio de la mínima acción").
Unos pocos cálculos
Uno de los grandes logros de Newton (obtenido simultáneamente también por Bernoulli y Leibniz) es el descubrimiento de la ecuación diferencial de la cicloide. Si indicamos como x e y las coordenadas de un punto genérico a lo largo de la cicloyde, y x+dx e y+dy a las de otro punto infinitamente cercano al primero, entonces:

Sabiendo esto, lo que hizo Newton fue encontrar la ecuación paramétrica de la cicloide para resolver el problema con su "garra"...
Imaginemos que el círculo generador de la cicloide (aquél que hacíamos rodar por el plano) tiene radio 1, y elijamos un punto cualquiera de la curva. Llamaremos P a tal punto, de nuevo x e y a sus coordenadas, y t a la medida en radianes del ángulo PÖB, igual a la abertura del arco PB. Entonces tenemos que
AB = PB
que
BC = PQ
y también que
PC = BQ
Luego:
x = AC = AB - BC = t - PQ = t - sen t
y también
y = PC = QB = OB - OQ = 1 - cos t
Cuando el círculo completa una rotación entera, el arco variará entre 0 y 2p. El punto definido por las coordenadas
(t-sen t, 1-cos t)
describe la cicloide.
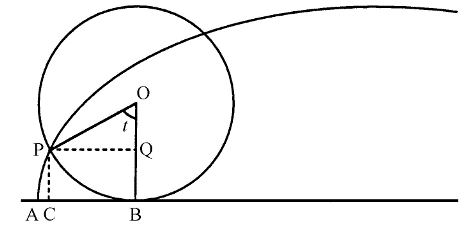
Diagrama de la ecuación paramétrica de Newton para las cicloides
Braquistócrono mecánico
La braquistócrona se puede visualizar muy bien con un aparato construido por el italiano Francesco Spighi en 1775.
El sistema de Spighi ilustra acabadamente la ley que Galileo descubrió y que inmortalizó en una carta a Guidobaldo del Monte. Es la misma que Bernoulli, Newton, Leibniz y Huygens utilizaron más tarde y de la cual hemos estado hablando en profundidad.
|
El braquistócrono de Spighi tiene un riel o surco de madera de forma cicloidal, apoyado en dos pies con tornillos para ajustarlos. Paralelo al cicloide hay otro canal recto que cruza la curva.
La inclinación del surco recto puede variarse, apoyándolo en los clavos que bordean la cicloide. Mediante una palanca se sueltan dos bolitas por los dos rieles simultáneamente. Sea cual sea la inclinación que le demos al surco recto, la bolita que se desplaza por la cicloide siempre llega antes al punto de encuentro.
Lamentablemente, no sabemos casi nada del constructor de este fascinante instrumento.
Nacido en Florencia, parece haber sido un constructor de muebles y armarios que terminó trabajando para el Imperiale e Regio Museum. Sus aparatos pueden verse hoy en el Gabinete de Física del mismo.

Vista posterior de un aparato similar.
El ocaso del viejo depredador
|
Luego de haber clavado tantas veces sus portentosas garras en el Universo, Newton cambió de profesión.
Sí, como lo leen.
Un buen día, su amigo Halley le recordó a la Reina que el más grande intelecto británico (y el hombre más inteligente de todos los tiempos, hasta donde sabemos hoy) era aún plebeyo. Ansiosamente, Su Majestad mandó llamar al felino y en el momento lo nombró Sir.
Era costumbre (y creo que lo sigue siendo) ofrecer un cargo público al hombre a quien se acababa de promover a la nobleza. La Reina le preguntó qué puesto le gustaría ocupar, pensando que Newton diría "Real Astrónomo de Su Majestad" o algo por el estilo.
Pero Newton se encargó, una vez más, de sorprender al mundo. Dijo: "Ehhhh... Me gustaría ser el Director de la Casa de Moneda". Y así lo nombraron.
Parece que le interesaba encontrar los métodos que usaban los falsificadores, determinar las proporciones de las aleaciones ("ley") utilizadas, etc.
Fue así que Sir Isaac, el viejo león, pasó la última cuarta parte de su vida sin preocuparse por la matemática, la física ni la gravedad, sino persiguiendo y ahorcando a los falsificadores de monedas de oro.
|
Sus últimos escritos, además, no versan ya sobre ciencia, sino sobre alquimia y astrología.
Sin embargo, cuando murió, en 1727, fue el primer científico en ser enterrado en la Abadia de Westminster, en reconocimiento al universo que, por sí mismo, él solito nos había permitido comprender correctamente.
Sobre su tumba han grabado la fórmula de desarrollo del binomio, que Newton descubrió:

El epitafio grabado bajo ella dice:
"H. S. E. ISAACUS NEWTON Eques Auratus, Qui, animi vi prope divina, Planetarum Motus, Figuras, Cometarum semitas, Oceanique Aestus. Suâ Mathesi facem praeferente Primus demonstravit: Radiorum Lucis dissimilitudines, Colorumque inde nascentium proprietates, Quas nemo antea vel suspicatus erat, pervestigavit. Naturae, Antiquitatis, S. Scripturae, Sedulus, sagax, fidus Interpres Dei O. M. Majestatem Philosophiâ asseruit, Evangelij Simplicitatem Moribus expressit. Sibi gratulentur Mortales, Tale tantumque exstitisse HUMANI GENERIS DECUS. NAT. XXV DEC. A.D. MDCXLII. OBIIT. XX. MAR. MDCXXVI".
("Aquí descansa Sir Isaac Newton, caballero que con fuerza mental casi divina demostró primero que nadie, con su brillante matemática, los movimientos y figuras de los planetas, los senderos de los cometas y el flujo y reflujo del océano. Investigó cuidadosamente las diferentes refracciones de los rayos de luz y las propiedades de los colores originados por aquellos. Intérprete laborioso, sagaz y fiel de la naturaleza, la Antigüedad y las Santas Escrituras, defendió en su filosofía la majestad del Todopoderoso y manifestó en su conducta la sencillez del Evangelio. Dad las gracias, mortales, al que ha existido así y tan grandemente como adorno de la raza humana. Nació el 25 de diciembre de 1642; falleció el 20 de marzo de 1727").
"H. S. E. ISAACUS NEWTON Eques Auratus, Qui, animi vi prope divina, Planetarum Motus, Figuras, Cometarum semitas, Oceanique Aestus. Suâ Mathesi facem praeferente Primus demonstravit: Radiorum Lucis dissimilitudines, Colorumque inde nascentium proprietates, Quas nemo antea vel suspicatus erat, pervestigavit. Naturae, Antiquitatis, S. Scripturae, Sedulus, sagax, fidus Interpres Dei O. M. Majestatem Philosophiâ asseruit, Evangelij Simplicitatem Moribus expressit. Sibi gratulentur Mortales, Tale tantumque exstitisse HUMANI GENERIS DECUS. NAT. XXV DEC. A.D. MDCXLII. OBIIT. XX. MAR. MDCXXVI".
("Aquí descansa Sir Isaac Newton, caballero que con fuerza mental casi divina demostró primero que nadie, con su brillante matemática, los movimientos y figuras de los planetas, los senderos de los cometas y el flujo y reflujo del océano. Investigó cuidadosamente las diferentes refracciones de los rayos de luz y las propiedades de los colores originados por aquellos. Intérprete laborioso, sagaz y fiel de la naturaleza, la Antigüedad y las Santas Escrituras, defendió en su filosofía la majestad del Todopoderoso y manifestó en su conducta la sencillez del Evangelio. Dad las gracias, mortales, al que ha existido así y tan grandemente como adorno de la raza humana. Nació el 25 de diciembre de 1642; falleció el 20 de marzo de 1727").
Sir Alexander Pope agregó un epitafio de su cosecha para Newton: "La Naturaleza y sus leyes yacían ocultas en la oscuridad. Dios dijo entonces: ´¡Sea Newton!´, y todo se iluminó".
Por cierto, John Collins Squire añade en broma: "Pero esto no terminó aquí... El Diablo gritó: ´¡Sea Einstein!´, y la situación anterior se restableció".
Así murieron las garras del viejo león, aquellas que habían comenzado a afilarse con el molino a ratón.

Mascarilla mortuoria de Newton, tomada del cadáver
Cuando Newton tenía siete años, el gato de la casa desapareció, y nunca volvió a los lugares que solía frecuentar.
La última vez que vieron al animal, casualmente, el niño Newton estaba construyendo un globo de aire caliente.
martes, 9 de octubre de 2012
Funciones hiperbólicas
En la geometría circular, encontramos las funciones trigonométricas, es por esto que la parametrización x=cos(t)e y=sen(t) forman una circunferencia de radio 1.
A causa de la semejanza que existe entre la circunferencia y la hipérbola, se plantea la cuestión de si habrá un conjunto de magnitudes o funciones que se correspondan con la hipérbola de la misma manera que las funciones circulares se corresponden con la circunferencia. Esas funciones existen y se denominan funciones hiperbólicas, es decir, seno hiperbólico, coseno hiperbólico, tangente hiperbólico, etc.
domingo, 7 de octubre de 2012
jueves, 13 de septiembre de 2012
Resumen 4.0 Cálculo Avanzado Pep 1
Versión corregida y mejorada de los contenidos correspondientes a la pep1.
lunes, 16 de julio de 2012
domingo, 8 de julio de 2012
Gauss y la integral Gaussiana
La Integral de Gauss

Función gaussiana  . El área encerrada bajo esa curva con el eje x es
. El área encerrada bajo esa curva con el eje x es 
 . El área encerrada bajo esa curva con el eje x es
. El área encerrada bajo esa curva con el eje x es 
En matemáticas la integral de Gauss, integral gaussiana o integral de probabilidad, es la integral impropia de la función gaussiana  sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es:
sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es:
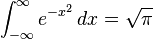
Esta integral tiene amplias aplicaciones, incluyendo normalización, en teoría de la probabilidad y transformada continua de Fourier. También aparece en la definición de la función error. A pesar de que no existe ninguna función elemental para la función error, como se puede demostrar mediante el algoritmo de Risch, la integral Gaussiana puede ser resuelta analíticamente con las herramientas del cálculo. O sea, no existe una integral indefinida elemental para pero si es posible evaluar la integral definida
pero si es posible evaluar la integral definida 
 sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es:
sobre toda la recta de los reales. Debe su nombre al matemático y físico alemán Carl Friedrich Gauss, y su valor es: 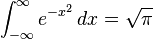
Esta integral tiene amplias aplicaciones, incluyendo normalización, en teoría de la probabilidad y transformada continua de Fourier. También aparece en la definición de la función error. A pesar de que no existe ninguna función elemental para la función error, como se puede demostrar mediante el algoritmo de Risch, la integral Gaussiana puede ser resuelta analíticamente con las herramientas del cálculo. O sea, no existe una integral indefinida elemental para
 pero si es posible evaluar la integral definida
pero si es posible evaluar la integral definida 
Cálculo de la integral
La forma más común de calcular la integral de Gauss en el plano R2 es mediante la integración doble en el sistema cartesiano de coordenadas, para después hacer un cambio de coordenadas a coordenadas polares y calcular el valor. Se procede de la siguiente manera:
sábado, 7 de julio de 2012
martes, 12 de junio de 2012
domingo, 3 de junio de 2012
Guía Pep 2 Cálculo avanzado.
Temas a tratar: Límites, continuidad, diferenciabilidad, derivadas, plano tangente.
Temas a tratar: Límites, continuidad, diferenciabilidad, derivadas, plano tangente.
Etiquetas:
Derivada Direccional,
Derivadas Parciales,
Diferenciabilidad,
Gradiente,
Límites,
Límites iterados,
Plano Tangente,
resumen,
Teorema Trayectorias
Suscribirse a:
Entradas (Atom)





